Pydata London 2017 and hyperopt
12 May 2017Last week I attended the PyData London conference, where I gave a talk about Bayesian optimization. The talk was based on my previous post on using scikit-learn to implement these kind of algorithms. The main points I wanted to get across in my talk were
- How the Bayesian optimization algorithm works; and
- How the algorithm can be used in your day-to-day work.
I have uploaded the slides to GitHub, and you can find them here.
It seems that there is interest in using these optimization methods, but that there are still a lot of difficulties in properly applying these algorithms. Especially the fact that you need to tune the optimization algorithm itself makes it non-trivial to apply these successfully in practice.
Sequential model-based algorithms (SMBOs) using hyperopt
In my talk, there was not a lot of time to dive into some of the more production-ready software packages for sequential model-based optimization algorithms. Lately, I spent some time working with the package hyperopt1, and its API is actually easy to use. It is also straightforward to make hyperopt work with scikit-learn estimators. By treating the model type as a hyperparameter, we can even build an optimization that not only optimizes the hyperparameters of a model, but also the type of model itself.
To understand the API of hyperopt, I’ll show how you can use hyperopt to tune a machine learning model, on an artificial data set.
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X, y = make_moons(n_samples=1000, noise=0.3, random_state=0)
X = StandardScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.4, random_state=42)
plot_data(X_train, X_test, y_train, y_test)
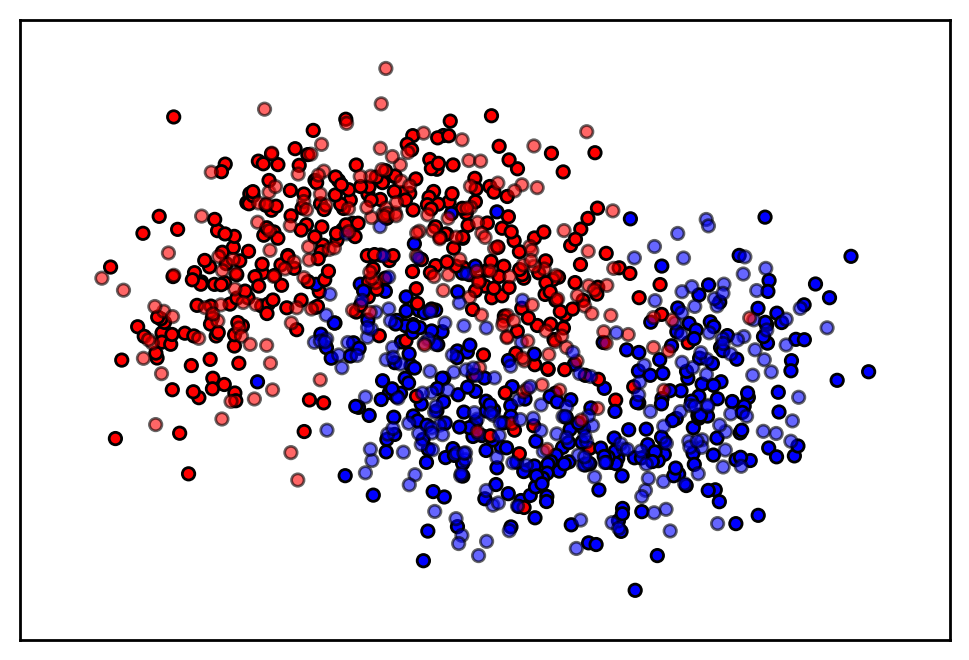
The goal is to estimate a classifier that can classify each sample into the correct group. We can use hyperopt to select both the optimal model, as well as the optimal parameters of the model. We need to give hyperopt the following:
- A search space for the hyperparameters.
- An objective function we want to optimize.
For the current use case, let’s say we want to decide between a k-nearest neighbors classifier, a support vector machine, and a gaussian process classifier.
The search space for hyperopt is similar to the search space in scikit-learn, and can be implemented by using either a list, or a dictionary. To build the search space, we will use hyperopts pchoice function, to tell hyperopt that we want to choose between different types of models.
from hyperopt import hp
from hyperopt.pyll import scope
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF, Matern
# We need to call scope.define on deterministic
# functions that we use in the search space
# definition
scope.define(KNeighborsClassifier)
scope.define(SVC)
scope.define(GaussianProcessClassifier)
# Sample the regularization parameter from a
# log-uniform distribution
C = hp.loguniform('svc_c', -4, 1)
# hp.pchoice takes a list of tuples (p, m), where
# p specifies the sampling probability of model m
search_space = hp.pchoice('estimator', [
(0.1, scope.KNeighborsClassifier(n_neighbors=1 + hp.randint('n_neighbors', 9))),
(0.1, scope.SVC(kernel='linear', C=C)),
(0.4, scope.SVC(kernel='rbf', C=C, gamma=hp.loguniform('svc_gamma', -4, 1))),
(0.4, scope.GaussianProcessClassifier(kernel=hp.choice('gp_kernel', [RBF(), Matern(nu=1.5), Matern(nu=2.5)])))
])
The above piece of code introduces multiple concepts from hyperopt:
- Prior distribution specification: hyperopt provides us with functions that we can use to describe the sampling distribution for the hyperparameters.
- Shared variables: The regularization parameter
Cis used in both the linear SVM, as well as the SVM with radial-basis kernel function. - Deterministic expressions in search spaces: In the search space definition, you can use more than the distribution functions provided by hyperopt (like
hp.choice,hp.loguniform) Deterministic functions (like scikit-learn estimators) can also be used, but they need to be wrapped usingscope.
Besides a search space, the other thing we need to provide is the objective function. In this setting, the objective function represents some measure of performance of the machine learning model.
from sklearn.metrics import accuracy_score
def objective_function(estimator):
estimator.fit(X_train, y_train)
y_hat = estimator.predict(X_test)
return -1 * accuracy_score(y_test, y_hat)
Note that, we could also have used the cross-validated accuracy score instead of the accuracy on a single hold-out set here.
Finally, hyperopt provides a function fmin that does the actual optimization. To get the optimal set of parameters, you simply call it as follows
from hyperopt import fmin, tpe
best = fmin(
fn=objective_function,
space=search_space,
algo=tpe.suggest, # This is the optimization algorithm hyperopt uses, a tree of parzen estimators
max_evals=50 # The number of iterations
)
print(best)
#>>> {'svc_c': 1.975771317797188, 'svc_gamma': 2.3274421992598877, 'estimator': 2}
In this case, hyperopt tells us that the optimal model is an SVM with RBF kernel, which shows a nice fit on the data set
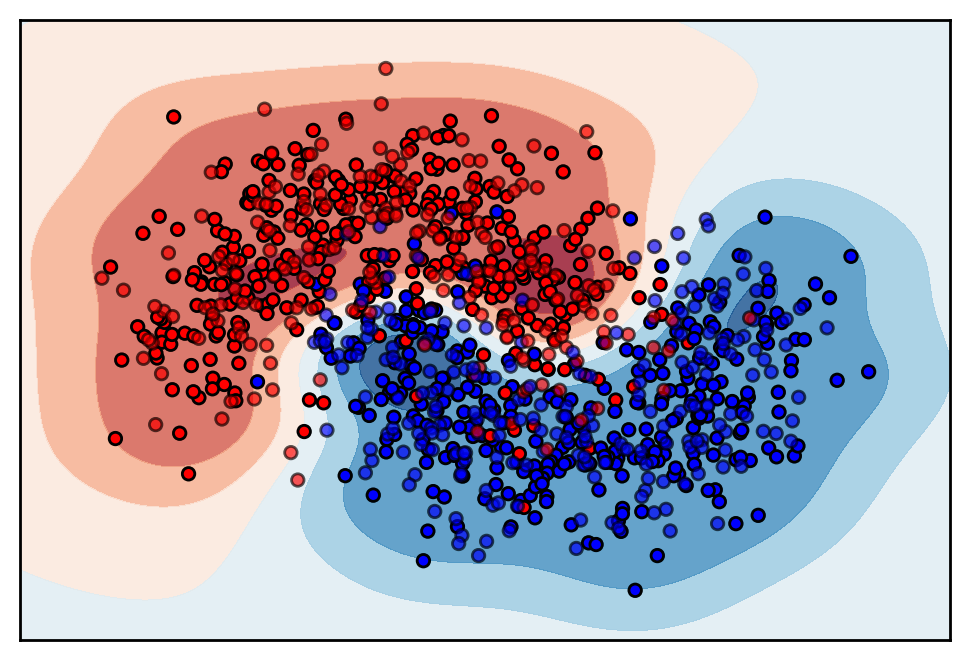
I’ve compiled the above code into a notebook that you can find here. I highly recommend reading the hyperopt paper1, if you want to get a better understanding of how hyperopt works.